Blackjack Expected Return

This calculator is a variation of the return & variance calculator. It includes all the functions of the standard calc, along with an hours of play estimate. Only blackjack is supported at this time. The player speed input and software selection pulldown are used to estimate your rate of play. Items must be sent back with our RMA number that we assign to each individual return – for our reference. United States Return requests must be within 30 days of receipt of the item. Items must be mailed within 5 business days of date return approval and label sent. International Return requests must be within 14 days of receipt of the item. The time has come. EV has lots of names: expectation, long-run expectation, LRE, fair value or expected value. Most people tend call it EV these days. EV isn’t a concept unique to blackjack.

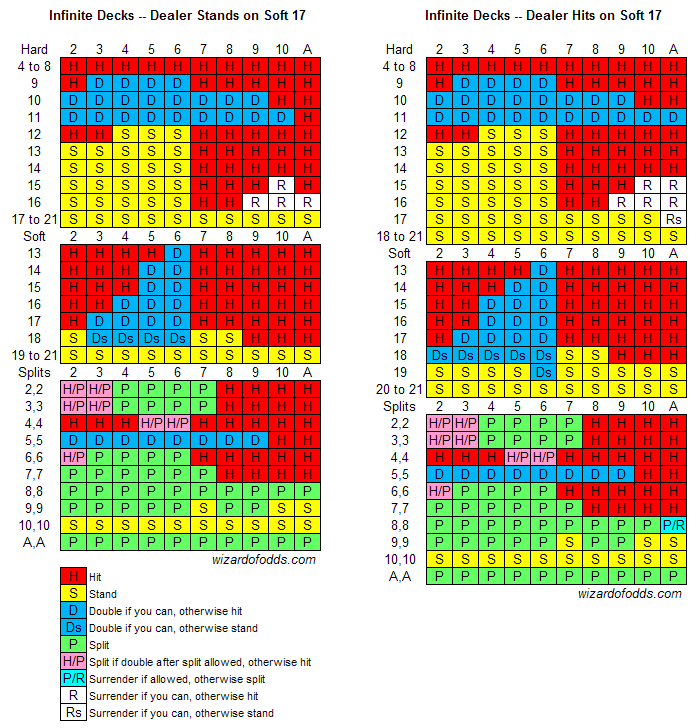
Expected values (EV) are what you will see in Appendix 9. If you look for dealer 10 against a player 10,9 for a single deck game the EV is 0.102517 if the player chooses to stand. This post is for people interested in how that calculation is done. Most people would try to calculate EV's in blackjack by simulations since it is so complex. The expected value changes on a per hand basis and depends on more than one factor. I assume what you're referring to is the basic strategy for Blackjack having a negative EV in a typically available variant of Blackjack. Here's the first rub, the composition of remaining cards is.

Expected return = 1 + Expected value.
Usually you refer to expected return in machine games, and expected value in table games. It seems silly, but I'm just trying to be consistent with the way everybody else does it.

Blackjack Expected Return

Expected return = 1 + Expected value.
Usually you refer to expected return in machine games, and expected value in table games. It seems silly, but I'm just trying to be consistent with the way everybody else does it.

Not presuming I know more than the Wizard about calculating odds, but I'm used to a different definition of 'return,' more in the classic business sense, like in 'investment return,' 'rate of return,' etc.
In that sense, wouldn't return be (Q1 - Q0) / Q0? E.g., I invested in MGM at $3 in Spring 09, cashed out at $8 that summer, a return of (8 - 3) / 3 = 167% (forgetting about annualization, time value, etc.).
Or, if you walk in with $100 and walk out with $95, your 'return' is (95 - 100) / 100 = minus-5%.
I guess statistical returns are a different animal than a financial return or something?

Expected return = 1 + Expected value.
Usually you refer to expected return in machine games, and expected value in table games. It seems silly, but I'm just trying to be consistent with the way everybody else does it.

It has to do with the 'N-to-1' vs. 'N-for-1' issue. Slot games payouts are universally N-for-1 - the lowest award on any paytable is 0, which is a loss, so 1 represents a push (e.g. Jacks or Better). The 'expected return' of a game, a.k.a. the payback percentage or the return-to-player (RTP) percentage, is the paytable times the probability distribution. That's going to be a number shy of 1.0, but can never be negative (since none of the pay values are negative).
Contrast with table game payouts. Those are usually N-to-1, so the lowest award on any paytable is -1 (a loss). When you take a table game paytable (even if it's just +1 and -1 for an even-money game like the passline) and multiply by the probability distribution, you get a number just shy of 0.0. So because the payout values are stated as -1 from how they'd be stated in slot games, so is the overall return percentage.

Blackjack Strategy Odds

Casino Odds Blackjack

Roulette Expected Returns